Home..

Classifying hate speech with LLM and multiSWAG

Lasse P. S. H. / May 2022

In 2017, the Danish Institute for Human Rights conducted an investigation revealing that \(15 \%\) of all comments in the Danish online public debate were classified as hate speech. Hate speech is defined as abusive or threatening speech directed against a particular group. According to the Cambridge Dictionary, it is:

public speech that expresses hate or encourages violence towards a person or group based on something such as race, religion, sex, or sexual orientation.

Public debate is a crucial component of our society and democracy. Therefore, it is essential to maintain a respectful tone when expressing political beliefs online to safeguard freedom of speech. Natural Language Processing (NLP) can be utilized to identify and classify hateful comments on social media.

This project explores how a Stochastic Weight Averaging Gaussian (SWAG) approach can further enhance the performance of the ELECTRA language model ¹. The model is trained on \(6000\) annotated text pieces collected from comment threads on public Facebook pages and groups.

SWAG

Stochastic Weight Averaging Gaussian (SWAG) emerged as a pioneering method for uncertainty representation in 2019 ². The approach involves a multi-step process wherein an initial model undergoes training, followed by further refinement using a Stochastic Gradient Descent (SGD) optimizer. During this training phase, crucial information about the weights at each step along the trajectory is meticulously preserved. This meticulous record-keeping allows for the computation of covariance, wherein an approximate distribution over the weights is established based on the SGD iterates.

Subsequently, this distribution serves as a basis for sampling new weights, thereby enabling exploration of a broader spectrum of the weight space. Notably, the covariance computation can be executed via two distinct methods: the SWAG-Diagonal approach or the Low Rank plus Diagonal Covariance Structure method. The SWAG-Diagonal method entails the calculation of diagonal elements within the covariance matrix, offering insights into the uncertainty inherent in individual weight parameters.

multiSWAG

MultiSWAG is a deep ensemble extension of SWAG ³. Ensemble learning combines several individual models to obtain better generalization performance by leveraging the diversity of multiple predictions. By training multiple models and sampling from each of their weight distributions, MultiSWAG explores a broader portion of the weight space compared to traditional SWAG. This increased exploration helps capture a wider range of possible solutions, improving uncertainty estimates and reducing overfitting. As a result, MultiSWAG offers a more robust and accurate representation of model uncertainty, leading to better performance on unseen data.

The Model

The model uses a pretranined-ELECTRA basemodel and a single dense layer with dropout and a prediction layer followed by a softmax function. The data have been split into \(60 \%\), \(30 \%\) and \(10 \%\) for training, testing and validation.

Training

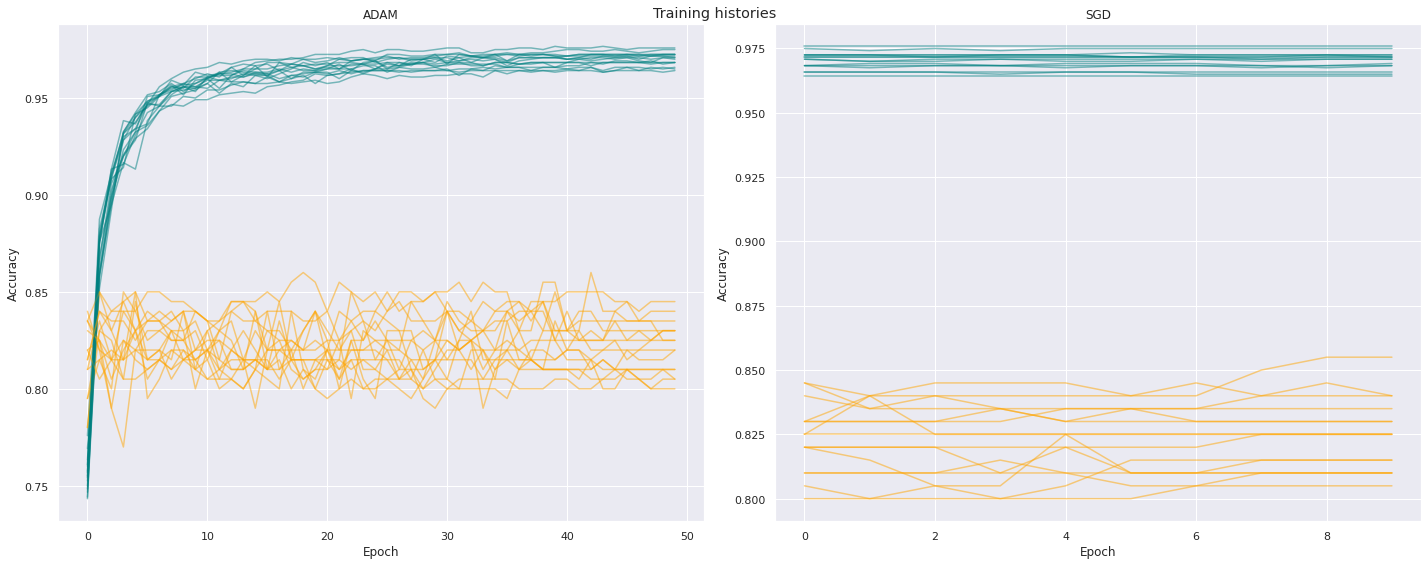
The following Figure shows the training histories for 10 models using the multiSWAG approach. The left side shows the initial step using ADAM optimizers. The right side shows the training histories for the SWAG approach using SGD optimizers.

Results

The following figure illustrates the weight space in the final dense layer of the model(s). Ten distinct models are sampled from each of the 10 different weight spaces, resulting in an ensemble of 100 models. The colormap represents the probability of a correct prediction for the sentence: “Er de fuldstændig ravende sindsyge i R? Landsforræderi.”

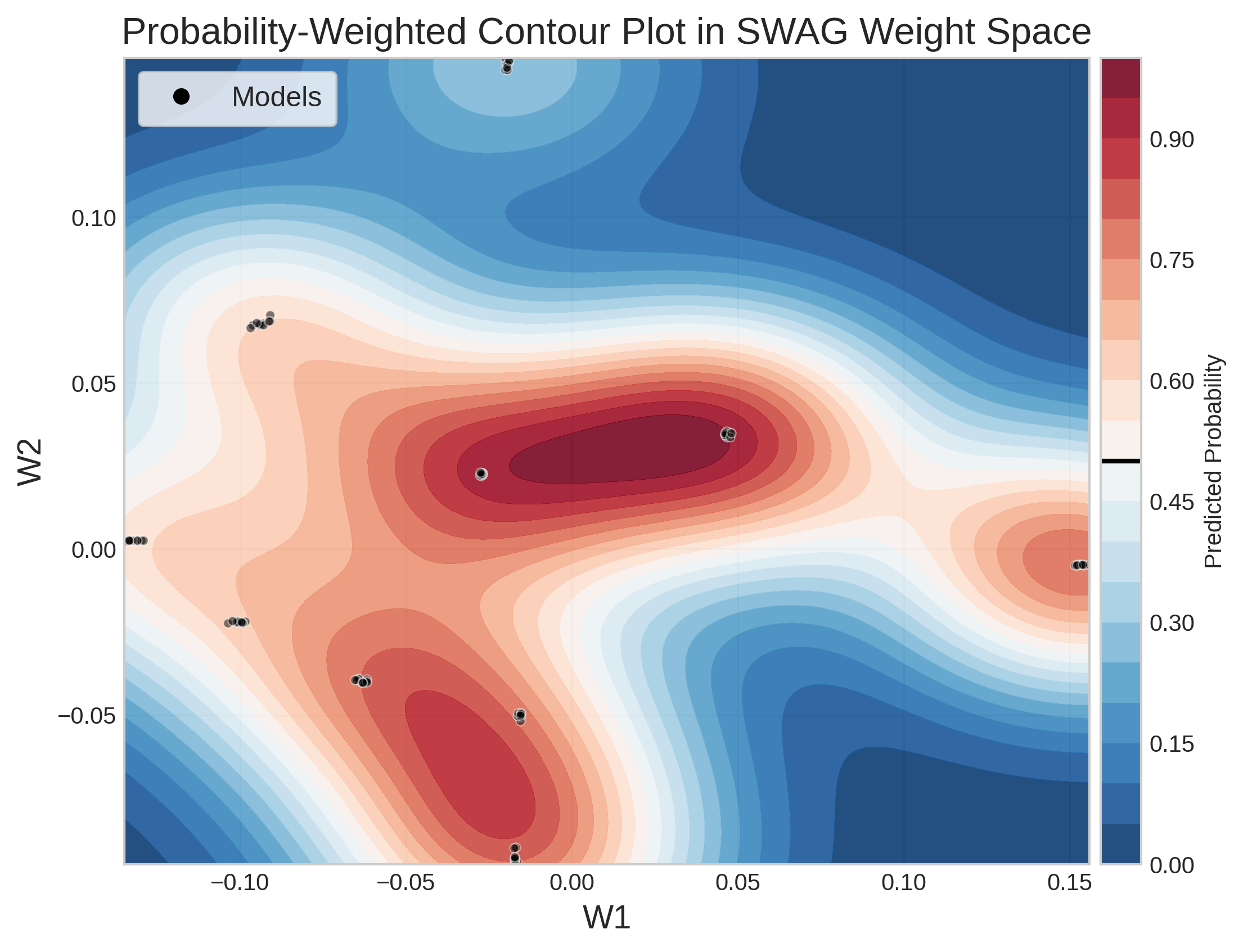\(60 \%\) of the models predicted the sentence as hatespeech.

The results shows that multiSWAG increases the performance of the base model.

	Precision	Recall	F1
Base Model	0.8457	0.8452	0.8433
SWAG	0.8413	0.8414	0.8400
MultiSWAG	0.8543	0.8546	0.8533

Table: Model macro averages.

---